众所周知，对一元二次方程 $ax ^ 2 + bx + c = 0, (a \neq 0)$，可以用下述方式求实数解：

• 计算 $\Delta = b ^ 2 - 4ac$，则:
  1. 若 $\Delta < 0$，则该一元二次方程无实数解；
  2. 否则 $\Delta \geq 0$，此时该一元二次方程有两个实数解 $x_{1, 2} = \frac{-b \pm \sqrt \Delta}{2a}$；
     • 其中，$\sqrt \Delta$ 表示 $\Delta$ 的算数平方根，即使得 $s^2 = \Delta$ 的唯一非负实数 $s$。
     • 特别的，当 $\Delta = 0$ 时，这两个实数解相等；当 $\Delta > 0$ 时，这两个实数解互异。

例如：

• $x ^ 2 + x + 1 = 0$ 无实数解，因为 $\Delta = 1 ^ 2 - 4 \times 1 \times 1 = -3 < 0$；
• $x ^ 2 - 2x + 1 = 0$ 有两相等实数解 $x_{1, 2} = 1$；
• $x ^ 2 - 3x + 2 = 0$ 有两互异实数解 $x_1 = 1, x_2 = 2$；

在题面描述中 $a$ 和 $b$ 的最大公因数使用 $\gcd(a, b)$ 表示。

例如 $12$ 和 $18$ 的最大公因数是 $6$，即 $\gcd(12, 18) = 6$。

现在给定一个一元二次方程的系数 $a, b, c$，其中 $a, b, c$ 均为整数且 $a \neq 0$。

你需要判断一元二次方程 $a x ^ 2 + bx + c = 0$ 是否有实数解，并按要求的格式输出。

在本题中输出有理数 $v$ 时须遵循以下规则：

• 由有理数的定义，存在唯一的两个整数 $p$ 和 $q$，满足 $q > 0$，$\gcd(p, q) = 1$ 且 $v = \frac pq$。
• 若 $q = 1$，则输出 {p}，否则输出 {p}/{q}，其中 {n} 代表整数 $n$ 的值；
• 例如：
  • 当 $v = -0.5$ 时，$p$ 和 $q$ 的值分别为 $-1$ 和 $2$，则应输出 -1/2；
  • 当 $v = 0$ 时，$p$ 和 $q$ 的值分别为 $0$ 和 $1$，则应输出 0。

对于方程的求解，分两种情况讨论：

1. 若 $\Delta = b ^ 2 - 4ac < 0$，则表明方程无实数解，此时你应当输出 NO；
2. 否则 $\Delta \geq 0$，此时方程有两解（可能相等），记其中较大者为 $x$，则：
   1. 若 $x$ 为有理数，则按有理数的格式输出 $x$。
   2. 否则根据上文公式，$x$ 可以被唯一表示为 $x = q_1 + q_2 \sqrt r$ 的形式，其中：
      • $q_1, q_2$ 为有理数，且 $q_2 > 0$；
      • $r$ 为正整数且 $r > 1$，且不存在正整数 $d > 1$ 使 $d ^ 2 \mid r$（即 $r$ 不应是 $d ^ 2$ 的倍数）；

此时：

1. 若 $q_1 \neq 0$，则按有理数的格式输出 $q_1$，并再输出一个加号 +；
2. 否则跳过这一步输出；

随后：

1. 若 $q_2 = 1$，则输出 sqrt({r})；
2. 否则若 $q_2$ 为整数，则输出 {q2}*sqrt({r})；
3. 否则若 $q_3 = \frac{1}{q_2}$ 为整数，则输出 sqrt({r})/{q3}；
4. 否则可以证明存在唯一整数 $c, d$ 满足 $c, d > 1, \gcd(c, d) = 1$ 且 $q _ 2 = \frac cd$，此时输出 {c}*sqrt({r})/{d}；

上述表示中 {n} 代表整数 $n$ 的值，详见样例。

如果方程有实数解，则按要求的格式输出两个实数解中的较大者。

否则若方程没有实数解，则输出 NO。

输入格式

输入的第一行包含两个正整数 $T, M$，分别表示方程数和系数的绝对值的上界；

接下来 $T$ 行，每行包含三个整数 $a, b, c$。

输出格式

输出 $T$ 行，每行包含一个字符串，表示对应询问的答案，格式如题面所述。

每行输出的字符串中间不应包含任何空格。

数据范围

对于所有测试数据有：$1 \leq T \leq 5000$，$1 \leq M \leq 10 ^ 3$，$|a|,|b|,|c| \leq M$，$a \neq 0$。

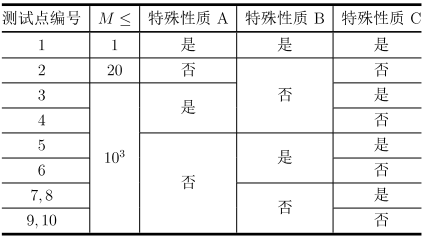
其中：

• 特殊性质 $A$：保证 $b = 0$；
• 特殊性质 $B$：保证 $c = 0$；
• 特殊性质 $C$：如果方程有解，那么方程的两个解都是整数。

输入样例：

9 1000
1 -1 0
-1 -1 -1
1 -2 1
1 5 4
4 4 1
1 0 -432
1 -3 1
2 -4 1
1 7 1

输出样例：

1
NO
1
-1
-1/2
12*sqrt(3)
3/2+sqrt(5)/2
1+sqrt(2)/2
-7/2+3*sqrt(5)/2